In landscape photography, it is often recommended to focus at the hyperfocal distance to maximize the scene in focus. But not everyone agrees (and we are not talking about artistic aspects here).
Harold Merklinger, a passionate photographer with a sound background in the sciences, wondered why his images taken with the hyperfocal distance did not really meet his expectations. In particular, he noticed that the more distant subjects often appeared substantially fuzzy [Merklinger 1992, Merklinger 2002]. The basic problem is illustrated by the following figure:
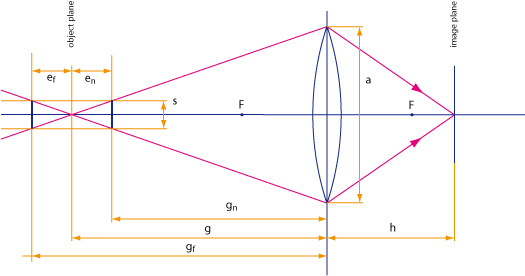
Consider a lens with a focal length f, which is focused at a certain distance. In this case, subject distance g and image distance h are adjusted according to the lens equation. As indicated by the purple lines, the rays emitted from a point in the subject plane towards the lens form a cone. The diameter of the cone is given by the aperture a of the lens.
If a subject is somewhat nearer or further away, it intersects the cone where it has some finite (i.e. non-zero) diameter s. If the subject is smaller than s, only a portion of the rays that reach the image plane at the original point will come from the subject; the recorded intensity will thus depend on some other content of the scene as well. In other words, the image of the subject gets blurred. The diameter s thus determines the smallest detail that the lens can (surely) resolve at this distance.
10.1 Minimum subject size
In the following, the diameter s is called the minimum subject size. It can be calculated as follows.
1. If an subject is located at a distance gn nearer to the lens, we get
| s / a | = | (g – gn) / g | (I1) |
by similar triangles. Solving for s gives
| s | = | (1 – gn / g) a | (I2) |
According to equation (I2), a subject located somewhere near the subject plane can be very small and still be resolved. On the other hand, a subject somewhere near the camera must be as large as the aperture of the lens.
2. If the subject is located at a distance gf farther away from the lens, a more serious problem appears. In this case, we get
| s / a | = | (gf – g) / g | (I3) |
Solving for s results in
| s | = | (gf / g – 1) a | (I4) |
According to equation (I4), the minimum subject size is thus not limited, but will grow proportional to the distance gf. Far away subjects may thus completely disappear, depending on their size and distance.
10.2 Merklinger’s approach
Fortunately, this problem can easily be avoided if we focus at infinity. In this case, all subjects in the scene are closer than the focus distance. Therefore, equation (I2) applies in all cases, and equation (I4) can be ignored. Furthermore, the fraction in equation (I2) disappears, and we get a surprisingly simple description of the minimum subject size
| s | = | a | (I5) |
Note that the aperture a of the lens is a distance which can be measured in mm, inches, or any other unit of length. With equation (A1), we can express a with the commonly used f-stop A and get
| s | = | f / A | (I6) |
For a camera focused at infinity, the minimum subject size that can be resolved thus depends on the focal length of the lens and the f-stop used, but not on the subject distance. This formula is used for the minimum subject size calculator.
For example, consider a lens with a focal length of 50 mm and the f-stop set to 8. The circle of confusion is assumed to be 0.033 mm. The hyperfocal distance is thus at about 9.6 m (31 ft). In this case, we get a minimum subject size of just 3 mm (0.1 in) at a distance of 5 m, but a whopping 600 mm (2 ft) at 1000 m. Anything smaller than that will more or less disappear. On the other hand, for the lens focused at infinity, the minimum subject size is about 6 mm (0.2 in), regardless if the subject is 5 m or 1000 m away. While the difference at 5 m is rather small, the effect at 1000 m can be quite dramatic.
The good news about Merklinger’s approach is that it does not only provide sharper images, but is also very easy to use. He actually recommends to focus at the most distant subject of interest, and adjust the f-stop to the size of nearby subjects that you still want to see. From equation (I6), the f-stop can easily be calculated as
| A | = | f / s | (I7) |
For a 50 mm lens and a targeted subject size of 10 mm, set your f-stop to 5. In his publications, Merklinger also investigates other uses of his approach, as in wildlife photography.
Note that equation (I6) describes a lower limit for the resolved subject size. Other limitations such as heat haze, lens diffraction and the finite resolution of the image sensor may have the effect that the resolved subject size is actually worse. However, this focusing strategy ensures that we can get as good as scene, lens and camera permit. Also note that neither the circle of confusion nor the size of the image sensor are considered, so results are valid for all kinds of cameras alike.
10.3 Hyperfocal distance revisited
Merklinger’s approach leaves us with the somewhat disturbing realization that the hyperfocal distance, although based on a seemingly valid theory about the depth of field, does not lead to optimal results. So what’s wrong?
Simply put, it is optimizing the wrong parameter. The aim of the hyperfocal distance is to ensure that the image of a point is never spread beyond a certain size on the image plane. However, as Merklinger has shown, this is not the main problem, as more distant subjects are completely smoothed out. In other words, the image of a point may be limited in size, but this doesn’t really matter if the point (or even a whole subject) is not visible. Actually, it makes much more sense to ensure that we can see it at all.
So do I ever use the hyperfocal distance? No, never.
