In macro photography, we want to get an image of a usually very small subject which is as detailed and therefore as large as possible. The magnification m is defined as the ratio of the image size H (on the sensor) to the subject size G (in the real world)
| m | = | H / G | (M1) |
The situation is illustrated in the following figure, which was already introduced for the lens equation.
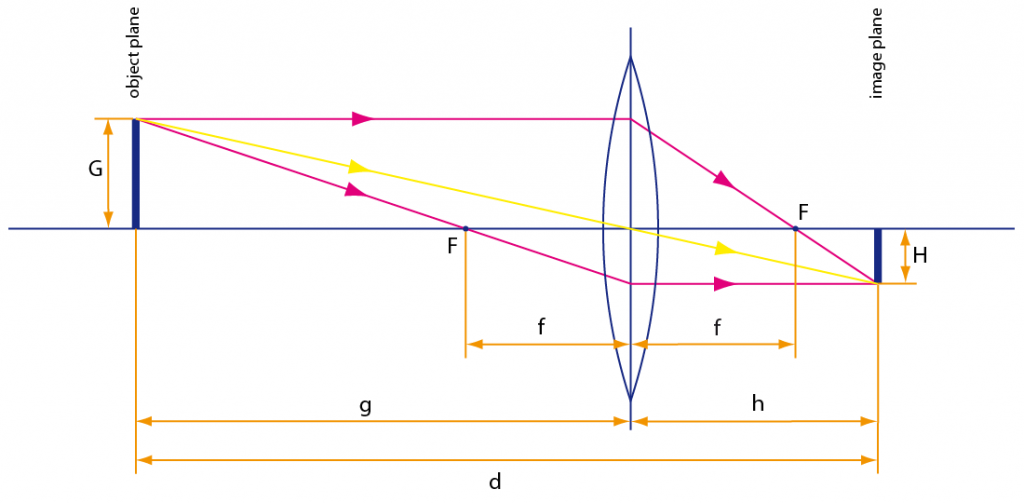
By similar triangles along the central ray (yellow), this is equivalent to
| m | = | h / g | (M2) |
For a given focus distance d, subject distance g and image distance h are given by equations (F7) and (F8), respectively, as
| g | = | d / 2 + r | (M3) |
| h | = | d / 2 – r | (M4) |
where r is defined as
| r | = | sqrt (d² / 4 – f d) | (M5) |
With equation (M2), we can now easily calculate the magnification m as
| m | = | (d / 2 – r) / (d / 2 + r) | (M6) |
This is the lens magnification equation used for the lens magnification calculator.
It is interesting to note that the magnification only depends on focal length f and focus distance d, but not on other factors such as aperture or the size of the image sensor. Results are thus valid for full-frame, crop and even smartphone cameras alike. However, for a given magnification, you can of course capture a larger subject with a larger sensor.
Since we are interested in the maximum magnification, it is clear that we must get as close to the subject as possible. Equation (F10) defines a lower bound for the minimum focus distance (MFD) of a lens as
| d | ≥ | 4 f | (M7) |
If the bound is reached, the root term (M5) becomes zero and the magnification as derived in equation (M6) becomes 1. This is indeed the maximum magnification of most macro lenses.
5.1 Approximation
If we solve the lens equation (L5) for h and substitute it into equation (M2), we get
| m | = | f / (g – f) | (M8) |
This formula looks much more appealing than equation (M6) and is thus sometimes published to calculate the lens magnification, but remember that we usually do not know the subject distance g, but only the focus distance d. For close-up situations, these may differ significantly.
However, if the subject is reasonably far away, i.e. the focal length f of the lens becomes insignificant compared to the focus distance d, we can approximate (g – f) by d and get
| m | ≈ | f / d | (M9) |
Double the focal length and you double the magnification. Easy to remember. Bear in mind though that the resulting figures are much too small for macro photography.
5.2 Notation
The magnification as derived by one of the given formulas is a positive real number. For example, for a focal length of 50 mm and a focus distance of 0.3 m (1 ft), we get a magnification of 0.27. This means that the size of the image H is 0.27 times (or 0.27×, 27%) of the size of the original subject G.
In photography, a commonly used notation for lens magnification is
| 1 | : | M | (M10) |
where M is calculated as the inverse of m. In our example, the magnification is 1 : 3.7, which indicates that the size of the image is 1 / 3.7 or about 1 / 4 of the size of the original.
The next section on lens extension tubes describes how a lens can be modified to provide a higher magnification.
