A converging lens is characterized by collecting parallel light rays in a focal point F. As a consequence, light emitted from a point in a subject plane (parallel to the lens, at a finite distance) is collected in a single point in a corresponding image plane (also parallel to the lens). For a thin converging lens, its thickness along the optical axis (drawn as a horizontal blue line) is small compared to its focal length.
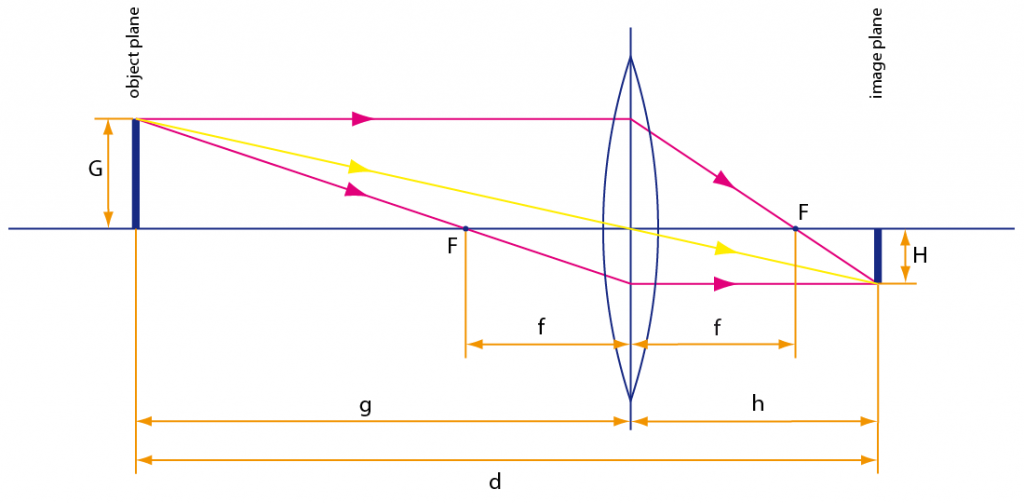
The lens equation describes the relation between focal length f of the lens, subject distance g between subject and lens and image distance h between lens and image sensor when the image of the subject appears sharp. It can be derived as follows.
By similar triangles along the purple ray passing through F left of the lens, we have
| G / (g – f) | = | H / f | (L1) |
Likewise, by similar triangles along the purple ray through F right of the lens, we get
| G / f | = | H / (h – f) | (L2) |
Solving both equations for G / H results in
| (g – f) / f | = | f / (h – f) | (L3) |
After some simple algebraic transformations, the equation looks like this
| g h | = | f h + f g | (L4) |
Finally, after division by f g h, we get the well-known form
| 1 / f | = | 1 / g + 1 / h | (L5) |
This equation is known as the lens equation or thin lens formula. See how g and h are adjusted when the lens is focused in the next section.
